天游线路检测中心 使用洛伦兹电子显微镜考虑磁性斯格明子

简介

　本研究的对象Skyrmion是英国核物理领域理论研究员Tony Skyrme于1960年左右提出的一种拓扑粒子结构模型[1]。后来，1989年，俄罗斯凝聚态物理学家Olexiy Bogdanov将斯格明子的概念引入电子自旋系统，并从理论上预测了它们在固体中的存在[2]。在磁性斯格明子中，图1如(a)中示意性所示，外部自旋和中心自旋方向颠倒，中间的自旋逐渐改变方向并像漩涡一样旋转[3,4]。涡旋的旋转方向称为斯格明子螺旋度，取决于材料的晶体结构（旋向性等）。此外，斯格明子中相邻的自旋彼此倾斜并形成立体角（图1（b）中的左图）。这个立体角被定义为自旋手性，并为穿过它的传导电子提供有效的磁场（涌现磁场）（图1（b）中的右图）[5]。这种出现的磁场与传导电子的自旋强烈相互作用，产生洛伦兹力[5,6]。传导电子因洛伦兹力而偏转，从而产生拓扑霍尔效应。同时，引发斯格明子霍尔运动[5]。随着斯格明子的运动，一种电磁感应也会产生涌现的能量场[5-7]。此外，斯格明子的特点是拓扑数为整数，一旦形成，它们就表现为亚稳态粒子，可以很容易地避免被材料中的杂质或晶体缺陷钉扎[8,9]。此外，驱动斯格明子的临界电流密度值为10⁶上午²，大约是驱动传统畴壁电流的1/100,000 [10]。由于上述性质的相继被揭示，斯格明子从凝聚态物理到潜在应用都充满了吸引力，近年来对斯格明子的研究迅速扩展。
　2009年，基于小角中子散射实验，在具有非中心对称B20立方晶体结构的MnSi中发现了由斯格明子形成的晶格。 MnSi具有手性（无反演对称性）晶体结构，因此其基态磁结构为螺旋结构。螺旋度（自旋扭曲方向）与晶体手性具有一对一的相关性[11,12]。螺旋的周期约为19 nm，与相邻自旋的铁磁交换系数与Jarosinski-Moriya相互作用系数之比成正比[3]。通过施加垂直于螺旋传播矢量的磁场，无论晶体取向如何，都可以观察到具有六方对称性的斯格明子晶格。然而，在小角中子散射实验中，斯格明子晶格出现在极窄的温度范围内，螺旋磁转变温度（T_N)仅在几开氏度的狭窄温度范围内观察到[3]。另一方面，蒙特卡罗模拟预测斯格明子晶格可以相对稳定地存在于二维薄膜样品中[4]。透射电子显微镜 (TEM) 样品必然是薄膜（通常小于 200 nm），因此使用透射电子显微镜进行观察被认为比中子衍射等其他技术更有效地捕获斯格明子。此外，利用洛伦兹电子显微镜（详细内容将在后面介绍）[13]和相位测量（强度输运方程法）[14]，还可以绘制纳米级磁化强度的空间分布图。 2010年，我们开发出具有相同B20型晶体结构的螺旋磁性材料Fe_0.5公司_0.5我们制作了硅薄片（约20 nm厚），在磁场下使用洛伦兹显微镜在电子显微镜中生成了斯格明子晶体，并成功进行了实空间观察[4]。在本文中，我们介绍了一种在磁场下使用洛伦兹电子显微镜产生磁性斯格明子的技术，然后在用磁场和电流驱动斯格明子的同时对它们进行原位观察。

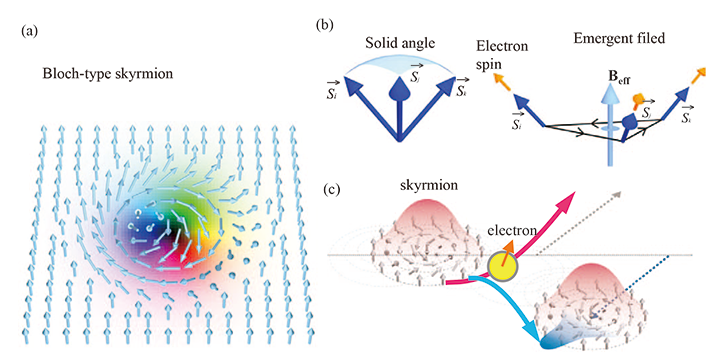[图1(a) Ploch型斯格明子示意图。颜色和箭头表示自旋分布。 （b）斯格明子中相邻自旋形成的立体角（左图）和相互倾斜的自旋环产生的涌现磁场（虚拟磁通量）（右图）示意图。 (c)拓扑霍尔效应和斯格明子霍尔运动示意图。当自旋极化电子（电流）通过斯格明子时，电子由于附在斯格明子上的涌现磁场而受到洛伦兹力，从而产生霍尔效应。由于洛伦兹力的反应，斯格明子本身经历霍尔运动。 】

磁场下的洛伦兹电子显微镜

　图2(a)显示通用洛伦兹电子显微镜示意图。样品的内部磁化强度和入射电子束之间的相互作用在垂直于电子束和样品的面内磁化强度的方向上产生洛伦兹力。这种洛伦兹力使电子束偏转，并且在欠焦和过焦表面上出现与磁畴壁相对应的明暗磁对比。这种在欠焦平面和超焦平面上形成图像的方法也称为散焦方法。标准洛伦兹电子显微镜的主要目的是观察铁磁材料的自发磁化。图2（b）和2（d）分别是180度畴壁、条纹畴壁和螺旋条纹结构的欠焦洛伦兹电子显微镜图像。对应于这些磁畴结构的面内磁化线轮廓如图1和2所示。 2(e)-2(g)。明暗对比代表反平行畴壁，它们之间的灰色区域对应于面内反平行畴（图2（b））或垂直（上下）畴（图2（c））。另一方面，图2（d）中的明暗交替的条纹结构代表波状（图2（g））磁化分布。磁化分布的周期约为5 nm。从这些结果可以看出，洛伦兹电子显微镜具有很高的空间分辨率（2 nm或更小），对于识别磁畴结构非常有效。然而，专用的洛伦兹电子显微镜，可以施加到样品上的磁场小于100毫特斯拉，其功能极其有限。另一方面，为了产生斯格明子，根据材料，需要在“与样品垂直的方向”施加几毫特斯拉到几百毫特斯拉的磁场。因此，利用传统的专用洛伦兹电子显微镜，很难对螺旋磁性材料施加垂直磁场以将其转变为斯格明子。另一方面，在通用电子显微镜中，大量电流通过透镜以获得高放大倍率和原子分辨率。这个大电流对样品施加强磁场。针对这一点，我们尝试使用通用电子显微镜（JEOL JEM-2100F和JEM-2800）生成斯格明子。然而，在通用电子显微镜的正常观察模式下，对样品施加约2T-3T的强磁场，因此样品的磁化强度通常会饱和。因此，斯格明子往往无法在如此强的磁场下存在。因此，我们决定通过减少透镜电流来减少施加到样品上的磁场。换句话说，他们成功地控制了透镜电流来产生斯格明子可以产生的磁场（从几十毫特斯拉到几百毫特斯拉）。通过减少镜头电流，可以增加焦距甚至相机长度。结果，衍射图案的放大倍数显着增加，从而更容易检测与样品中自发磁化相对应的电子束偏转。换句话说，通过减少物镜电流，产生斯格明子，并且可以对斯格明子进行洛伦兹观察。在本研究中，我们利用装置中安装的“自由透镜控制”功能，通过控制磁透镜的电流来控制施加到样品上的磁场，并找到了斯格明子形成的条件。此外，在这样的磁场下使用洛伦兹电子显微镜进行原位观察，使斯格明子可视化。


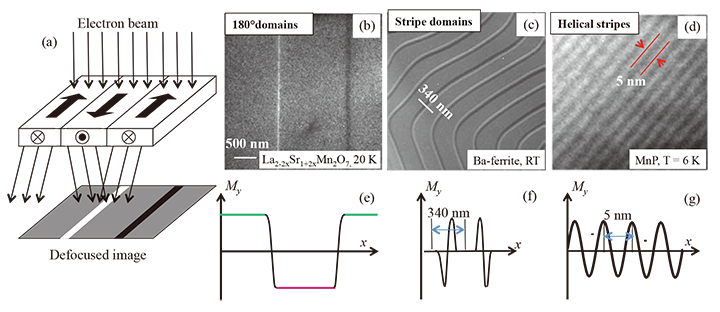[图2(a)洛伦兹电子显微镜示意图。当入射电子束穿过铁磁材料时，电子因磁性材料磁化引起的洛伦兹力而偏转。当电子显微镜聚焦在样品上时，不会出现偏转的影响，但在电子显微镜离焦的观察平面（散焦平面）上，电子密度会因偏转而变得更密或更密。 (b)在180°磁畴壁中出现明暗线性对比度，并且(e)所示的面内磁化强度分布表明这些磁畴壁是布洛赫磁畴壁。 (c)和(f)是与布洛赫磁畴壁反平行交替排列的垂直磁畴(也称为条状磁畴)的洛伦兹图像(c)和面内磁化分布(f)。 (d)和(e)是螺旋磁结构(d)的洛伦兹图像及其面内磁化强度分布(e)。 】

实验

本文介绍的观察用单晶（FeGe）和多晶（Fe_0.5公司_0.5Ge, Co-Zn-Mn)样品。通过机械抛光和离子抛光(Gatan Inc制造的PIPS)制备用于电子显微镜的薄样品。^TM，型号691)，将厚度减少至200 nm或更小。此外，使用聚焦离子束加工装置（日立FB2100）来制造用于施加电流的微型器件。将处理后的样品安装在可以用液氦冷却的电子显微镜支架(Gatan Inc制造的ULTST)或电流观察用支架(Gatan Inc制造的HCHST)上。使用场致发射电子显微镜(JEM-2800或JEM-2100F，由天游线路检测中心制造)作为观察电子显微镜。电子显微镜观察时，利用“自由透镜控制”功能使物镜电流从零逐渐增加，在施加垂直于样品表面的磁场的同时观察磁畴结构。使用配备霍尔探针的支架测量电子显微镜样品周围的磁场。为了获得斯格明子的磁化强度分布，我们采用相位测量法（强度输运方程法）（使用QPt（HREM Research Inc制造）软件计算）[14]提取正焦点（欠焦和过焦）拍摄的两张洛伦兹电子显微镜图像的相位变化，并绘制磁化强度的空间分布图。

斯格明子螺旋度的测量

　如上所述，斯格明子中螺旋的方向称为斯格明子螺旋度。在具有破缺空间反演对称性的B20型晶体结构的手性晶体中，由于自旋轨道相互作用（Jarosinski-Moriya相互作用[17]），证实基态是螺旋磁结构[18]。磁场下感应的斯格明子的螺旋度由手性晶体的手性决定，反映了 Jarosinski-Moriya 相互作用的符号 [11, 12]。换句话说，有两种模式：一种是逆时针（顺时针）斯格明子螺旋性对应于晶格的左手（右手）手性，另一种是对应关系相反。这种关系是图3如(a)-3(b)所示。此外，如图3（c）的示意图所示，由于入射电子束会聚在过聚焦像面上，逆时针斯格明子可以观察到亮点，而顺时针斯格明子由于电子束发散而可以观察到暗点。
　图3（d）显示Co-Zn-Mn和Fe分别具有左手性和右手性_0.5公司_0.5这是在Ge中观察到的单个斯格明子的超焦洛伦兹电子显微镜图像。作为真实空间图像观察到如图3(c)示意性所示的亮点或暗点。此外，我们提取了从正焦点移除的两个散焦（欠焦和过焦）洛伦兹电子显微镜图像的相位变化，并绘制了磁矩的空间分布。结果如图3(e)所示。彩色和白色箭头代表面内磁化强度的大小和方向。在黑色区域，磁化的面内分量极弱，导致垂直磁化。这些斯格明子具有图3(b)中示意性所示的结构，并且已经表明它们的螺旋度分别是逆时针和顺时针的。


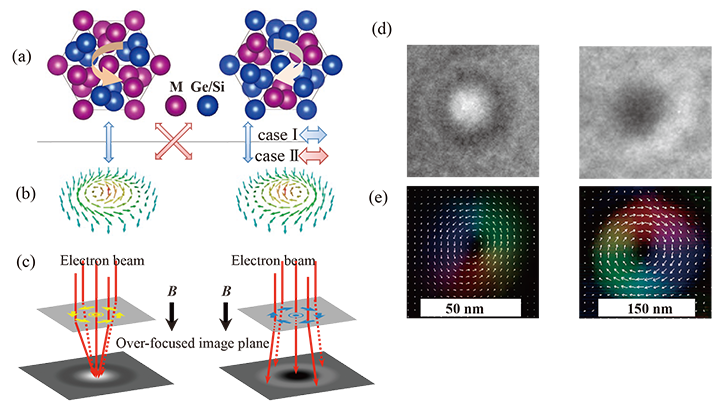[图3（a）具有右手性（左图）和左手性（右图）手性的晶体结构示意图。 M表示过渡金属。 (b)不同斯格明子螺旋度的斯格明子磁矩排列示意图。 (c)用洛伦兹电子显微镜观察(b)所示的斯格明子时，在过焦像面上电子束的偏振所产生的会聚像(具有逆时针螺旋性的斯格明子)和发散像(具有顺时针螺旋性的斯格明子)的示意图。 B 是施加的磁场。 (d) 具有逆时针（左）或顺时针（右）螺旋度的斯格明子的过焦洛伦兹电子显微照片。 （e）通过相位测量方法（强度输运方程）获得的具有逆时针（左图）或顺时针（右图）螺旋度的斯格明子的面内磁矩分布。箭头和颜色表示磁矩的方向和大小。黑色代表垂直磁矩。 ]

通过施加弱磁场生成斯格明子晶体

到目前为止，我们已经介绍了一种结合磁场下洛伦兹电子显微镜和电子束相位测量方法来实空间观察单个斯格明子并测量斯格明子螺旋度的方法[14]。在自旋电子学领域，单个斯格明子作为信息位引起了极大的兴趣。接下来，我们尝试在材料中生成斯格明子晶体，以获得高密度斯格明子晶体带来的巨拓扑空穴效应[5]。我们感兴趣的材料是 FeGe，一种具有高磁有序温度 (~280K) 和 B20 型螺旋结构的磁性材料。 FeGe的260 K洛伦兹电子显微镜图像分析结果图4如(a)和4(b)所示。无磁场条件下的磁化分布为螺旋自旋排列（图4（a）），螺旋自旋的重复周期和螺旋矢量的传播方向分别为70 nm和<110>。当对样品施加100 mTesla垂直磁场时，形成具有逆时针螺旋性的斯格明子三角晶格。根据在不同温度和磁场下观察到的洛伦兹电子显微镜图像，两种不同厚度的FeGe薄片的磁结构相图分别绘制在图4（c）和图4（d）中。这将螺旋磁结构、具有多个螺旋传播矢量的磁结构、斯格明子晶体或铁磁单畴的相界表示为温度-磁平面上的斯格明子密度等值线图。可以看出，两相图明显不同。首先，向斯格明子晶体转变过程中磁场的大小是不同的。较薄的样品中铁磁转变场更强。这是因为薄的样品几何形状增加了退磁场，并且需要大的外加磁场来感应铁磁态。此外，斯格明子晶相的温度范围也不同。当样品厚度变得与斯格明子直径一样厚时，斯格明子相仅存在于刚好低于螺旋转变温度的狭窄窗口区域中。相反，当样品厚度变得小于斯格明子直径时，斯格明子晶相在温度-磁平面上展开并成为更稳定的实体。


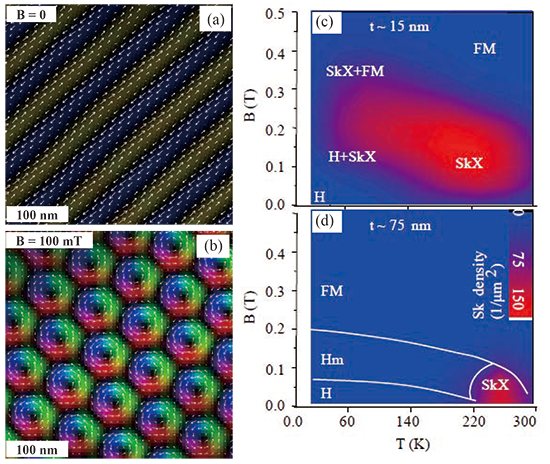[图4（a）-（b）使用强度传输方程方法获得的螺旋磁结构（a）和斯格明子晶体（b）。 (c)-(d) 在不同磁场或温度下，通过洛伦兹电子显微镜获得厚度为 15 nm (c) 和 75 nm (d) 的 FeGe 薄片的磁相图。该相图显示了螺旋磁结构 (H)、多个螺旋传播矢量 (Hm) 的混合状态、斯格明子晶体 (SkX) 和铁磁单磁畴 (FM) 的相界，作为斯格明子密度的等值线图。 ]

通过电流驱动斯格明子晶体

　为了用电流驱动斯格明子，我们通过使用聚焦离子束加工装置加工 FeGe 单晶（一种螺旋磁性材料）来制造微型器件 [10]。该微型器件由用于洛伦兹电子显微镜的 FeGe 薄片、支撑薄片的厚 FeGe 块和电极部分组成。在洛伦兹电子显微镜中，通过将 100 毫特斯拉垂直磁场施加到器件的薄区域（约 100 nm 厚），创建了晶格间距约 70 nm 且具有六重对称性的斯格明子晶体 (图5(a))。图 5(b)-5(f) 是在 273K（略低于磁转变点）的温度下向器件施加电流时获得的洛伦兹电子显微镜图像。电流（从图像底部到顶部的方向）逐渐增加到不会因焦耳热而引起磁转变的值。洛伦兹图像揭示了以下内容。 (1)电流密度为42A/cm²时，斯格明子晶体开始移动。 (2) 随着电流密度的增加，斯格明子晶体沿着与施加电流方向倾斜的方向平移，电流密度增加到49A/cm²之上，大多数斯格明子从观察视野中消失（图5（f））。由以上结果可知，驱动斯格明子所需的临界电流密度为42A/cm²，比传统畴壁驱动所需的阈值电流密度小五个数量级以上[10]。这可以说是开发下一代节能磁存储器件的重要特征。


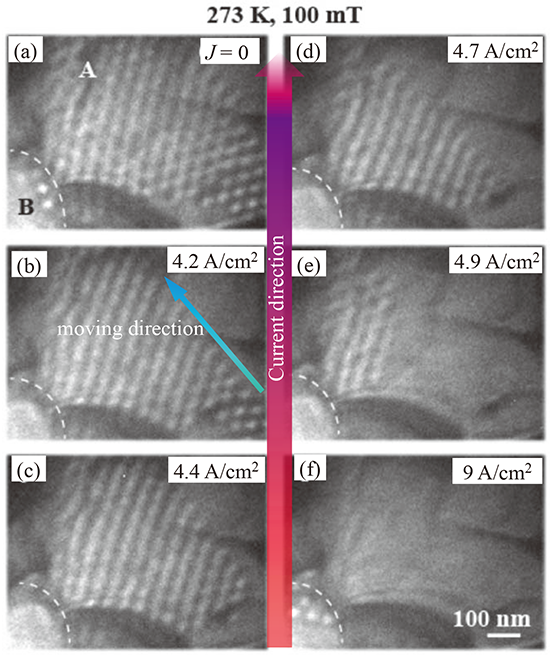[图5 电流连续通过斯格明子晶体时洛伦兹电子显微镜图像的变化。箭头分别表示当前应用的方向（长箭头）和斯格明子运动的方向（短箭头）。 ]

最后

通过利用洛伦兹电子显微镜，我们在世界上第一个成功地巧妙地控制具有B20晶体结构的螺旋磁性材料薄片中的物镜电流，以产生单螺旋斯格明子和斯格明子晶格，并在真实空间中以洛伦兹电子显微镜图像的形式观察（可视化）它们。此外，通过制作微型器件并用电流驱动斯格明子晶体，我们能够通过真实空间的原位观测来了解斯格明子的动态特性。
　基于薄膜样品的透射洛伦兹电子显微镜对于分析斯格明子等拓扑自旋纹理非常有效，我们预计它在未来将继续做出重大贡献。

致谢

这项研究是 RIKEN、东京大学和国立材料科学研究所 (NIMS) 之间的合作。参与本文介绍的研究成果的合作研究人员（名称省略）有 Naoto Naganaga (RIKEN)、Naoya Kanazawa (东京大学)、Motohiro Shibata (东京大学)、Daisuke Morikawa (RIKEN)、Yusuke Tokunaga (The University of Tokyo)、Kojiro Taguchi (RIKEN)、包括 Yoshifumi Nose (东京大学)、Yuki Shiomi （东北大学）、Shintaro Ishiwata（东京大学）、Koji Kimoto (NIMS)、Weizhu Zhu (NIMS)、Takuro Nagai (NIMS)、Toru Hara (NIMS) 和 Yoshio Matsui (NIMS)。我们还收到了 Takahisa Arima（东京大学）、Masashi Kawasaki（东京大学）、Kazuo Ishizuka（HREMResearch Inc）和 Toru Asaka（名古屋工业大学）的有用建议。我们还得到了 RIKEN Emergence Center 的 Mari Ishida 和 Kikitsu 的实验支持。
　在进行这项研究时，我要向参与 JEM-2800 安装的 天游线路检测中心 工程师表示诚挚的谢意，特别是 Noriaki Endo、Mikio Yada、Katsunori Nakamura 和 Takahiro Adachi。

参考文献

1. T。斯凯尔梅，核物理 31, 556 （1962）.
2. A N Bogdanov 和 D A Yablonskiî,俄罗斯物理学 JETP . 68, 101 （1989）.
3. S。米尔鲍尔，等人，科学 323, 915 （2009）.
4. X。于Z，等人，《自然》 465, 901 （2010）.
5. N。 Nagaosa 和 Y Tokura，自然纳米技术。 8, 899 （2013）.
6. T。舒尔茨，等人，《自然》。物理. 8, 301 （2012）.
7. N。金泽,等人，物理学。莱特牧师 106, 15603 （2011）.
8. F。乔尼茨，等人，科学 330, 1648 （2010）.
9. J。岩崎，等人，《自然纳米技术》. 8, 742 （2013）.
10. X。 Z Yu 等人，自然社区 . 3:988 （2012）.
11. S。柴田等人，自然纳米技术 . 8, 723 （2013）.
12. D。 Morikawa、K Shibata、N Kanazawa、X Z Yu 和 Y Tokura，物理。修订版. B 88, 024408 （2013）.
13. L。赖默和 K 科尔，透射电子显微镜（施普林格，2008）.
14. K。石冢和 B奥尔曼：J。电子显微镜. 54, 191 （2005）.
15. X。 Z Yu 等人，自然。马特 . 10, 106 （2011）.
16. Y。德永,等人，自然通讯。正在出版（2015）。
17. 我。贾洛辛斯基,J。物理。化学。固体 4, 241 （1958）.
18. M。内田、Y Onose、Y 松井和 Y Tokura，科学 311, 359 （2006）.